The genetic relatedness between individual parasite haplotypes and
among parasite populations has several practical uses in the study of
malaria. For example, relatedness information can help determine the
geographic origin of imported infections, define the extent to which
parasites are dispersing or are contained within landscapes, and
identify whether specific strains are being selected for over time.
Relatedness information is also very helpful in understanding
longitudinal (within-individual) infection dynamics. In the case of
P. vivax, for example, it can distinguish whether infection
represents newly acquired parasites, recrudescence after treatment, or
relapse from longer-lasting hypnozoite reservoirs. Relatedness
information can also help resolve polyclonality signals, i.e., clarify
the number of different haplotypes co-infecting individual patients.
Relatedness is defined as the probability that, at any locus in the
genome, the alleles sampled from two different individuals are identical
by descent (\(IBD\)). Genetic markers
used for this purpose include SNPs, microsatellites, and (increasingly)
amplicon micro-haplotypes (MHAP). Relatedness can be estimated using a
Hidden Markov Model approach implemented in the R package
paneljudge (see mathematical framework in AR Taylor
et al. 2019). In this package, relatedness (\(r\)) is estimated as a function of the
haplotype of the two sampled parasites (\(Y^{(i)}\) and \(Y^{(j)}\), where \(i\) and \(j\) denote two different sampled genotypes
from the population), the frequency of the alleles in the population
(\(f_t(g)\), where \(t\) denotes locus), the physical distance
(\(d_t\), in base-pairs) between
successively analyzed loci (\(t-1\) and
\(t\)), the recombination rate (\(\rho\)), a switching rate of the Markov
chain (\(k\)), and a constant
genotyping error rate (\(\varepsilon\)).
Pairwise relatedness comparisons between categories
For this report all possible pairwise IBD comparisons between samples
from different categories of Variable1 and Variable2 are computed, and
the results are shown in the following table:
source('~/Documents/Github/intro_to_genomic_surveillance/docs/functions_and_libraries/amplseq_required_libraries.R')
source('~/Documents/Github/intro_to_genomic_surveillance/docs/functions_and_libraries/amplseq_functions.R')
#sourceCpp('~/Documents/Github/intro_to_genomic_surveillance/docs/functions_and_libraries/hmmloglikelihood.cpp')
Read the ampseq_object in csv format:
ampseq_object = read_ampseq(file = '~/Documents/Github/intro_to_genomic_surveillance/docs/data/Pfal_example/Pfal_ampseq_filtered',
format = 'csv')
Run the function pairwise_hmmIBD:
pairwise_relatedness_table = '~/Documents/Github/intro_to_genomic_surveillance/docs/data/Pfal_example/pairwise_relatedness.csv'
if(!file.exists(pairwise_relatedness_table)){
pairwise_relatedness = NULL
nChunks = 500
for(w in nChunks){
start = Sys.time()
pairwise_relatedness = rbind(pairwise_relatedness,
pairwise_hmmIBD(ampseq_object, parallel = TRUE, w = w, n = nChunks))
time_diff = Sys.time() - start
print(paste0('step ', w, ' done in ', time_diff, ' secs'))
}
write.csv(pairwise_relatedness,
'~/Documents/Github/intro_to_genomic_surveillance/docs/data/Pfal_example/pairwise_relatedness.csv',
quote = FALSE,
row.names = FALSE)
}else{
pairwise_relatedness = read.csv(pairwise_relatedness_table)
}
Plot the distribution of relatedness between sites using the function
plot_relatedness_distribution
plot_relatedness_distribution_between = plot_relatedness_distribution(
pairwise_relatedness = pairwise_relatedness,
metadata = ampseq_object@metadata,
Population = 'Subnational_level2',
fill_color = rep('gray50', length(unique(ampseq_object@metadata[['Subnational_level2']]))*(length(unique(ampseq_object@metadata[['Subnational_level2']]))-1)/2),
type_pop_comparison = 'between',
ncol = 3,
pop_levels = NULL
)
View(plot_relatedness_distribution_between$relatedness)
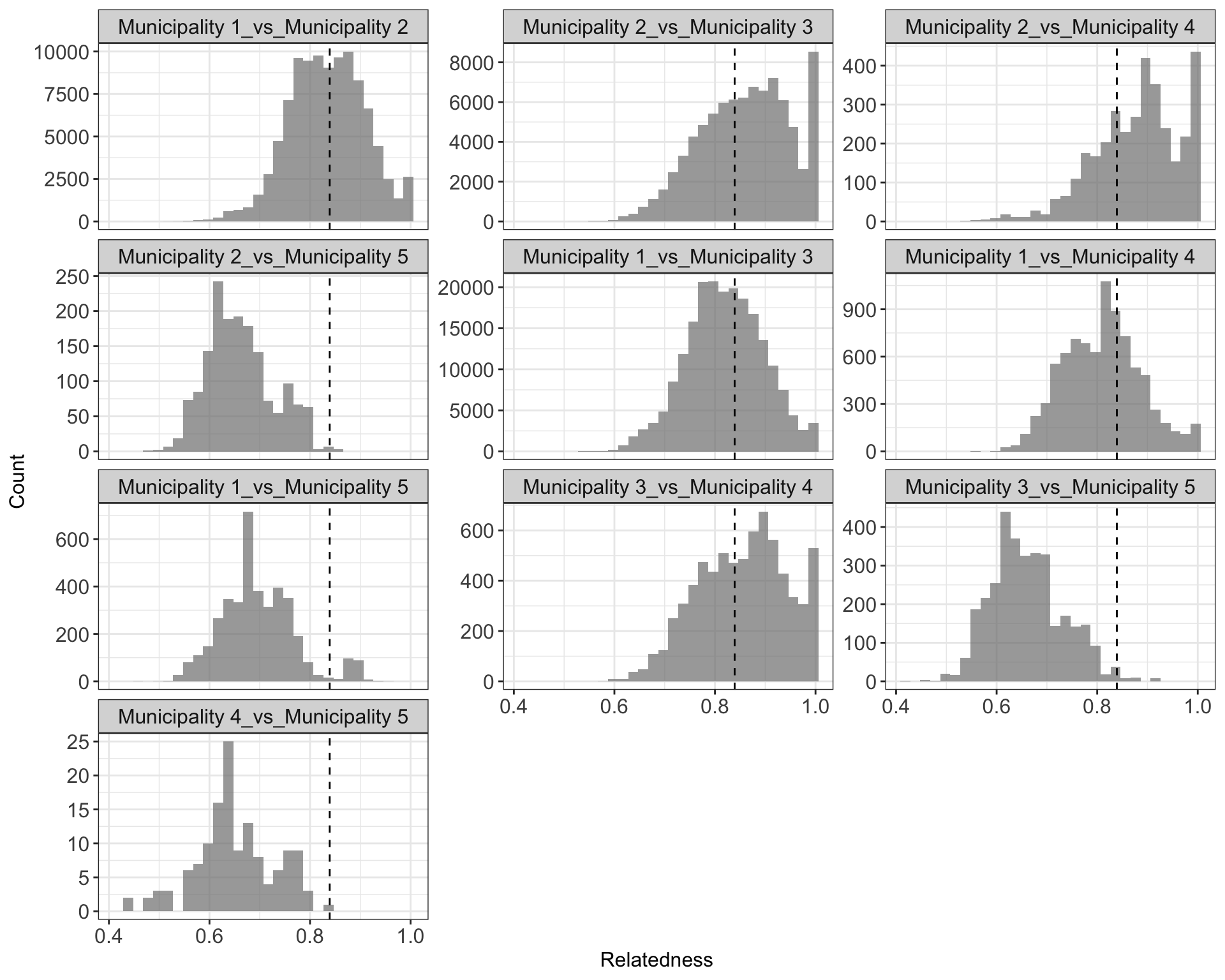
The distribution of pairwise genetic relatedness values is presented
using histograms as follows:
plot_relatedness_distribution_between$plot
Fraction of highly related comparisons between categories of
Variable1 over Variable2
Highly related pairwise comparisons between categories in
Subnational_level2 and Quarter_of_Collection are also counted and
proportions with their 95% CI (Fisher exact test) are calculated.
plot_frac_highly_related_overtime_between = plot_frac_highly_related_over_time(
pairwise_relatedness = pairwise_relatedness,
metadata = ampseq_object@metadata,
Population = c('Subnational_level2', 'Quarter_of_Collection'),
fill_color = rep('gray50', length(unique(ampseq_object@metadata[['Subnational_level2']]))*(length(unique(ampseq_object@metadata[['Subnational_level2']]))-1)/2),
threshold = 0.99,
type_pop_comparison = 'between',
ncol = 3,
pop_levels = NULL)
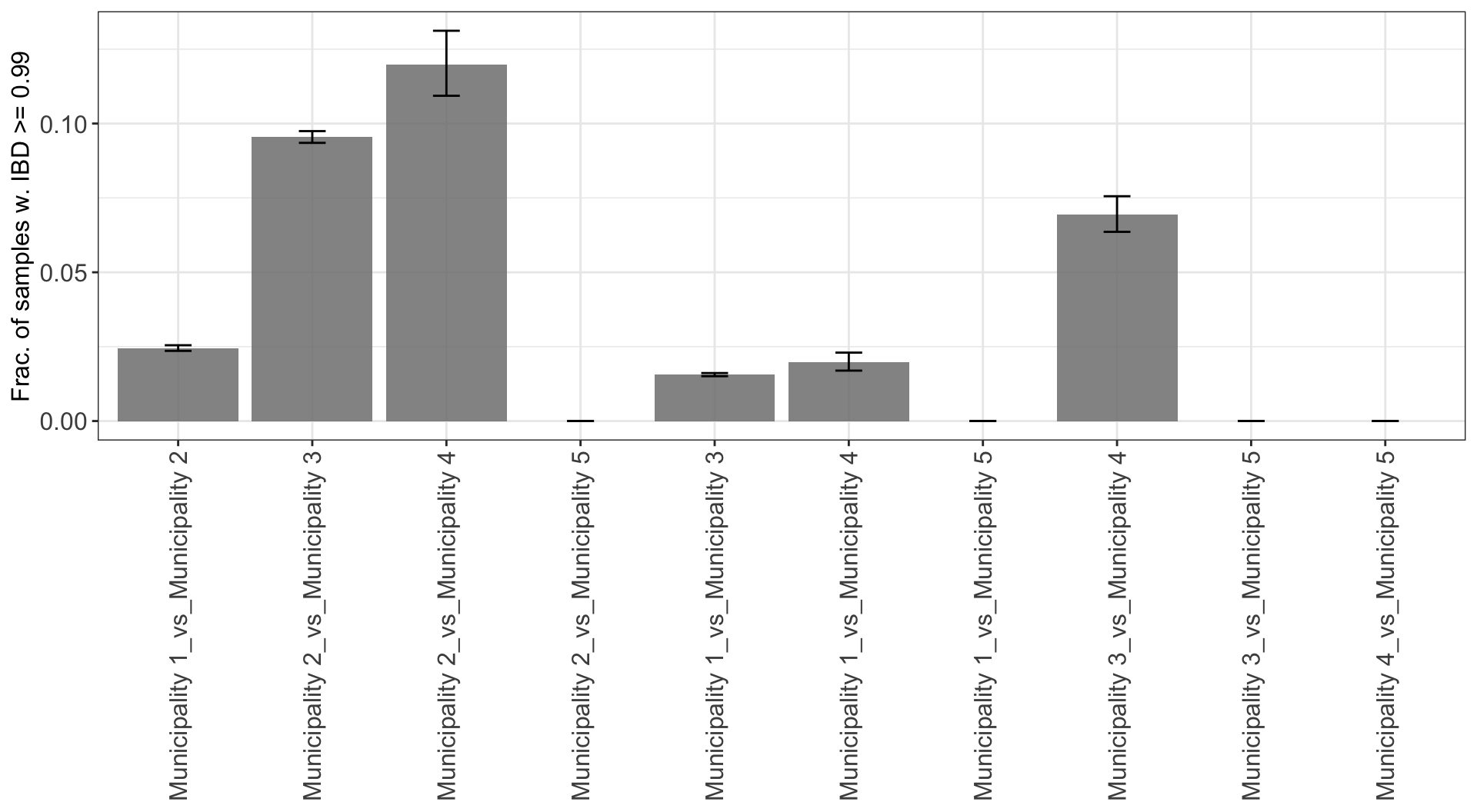
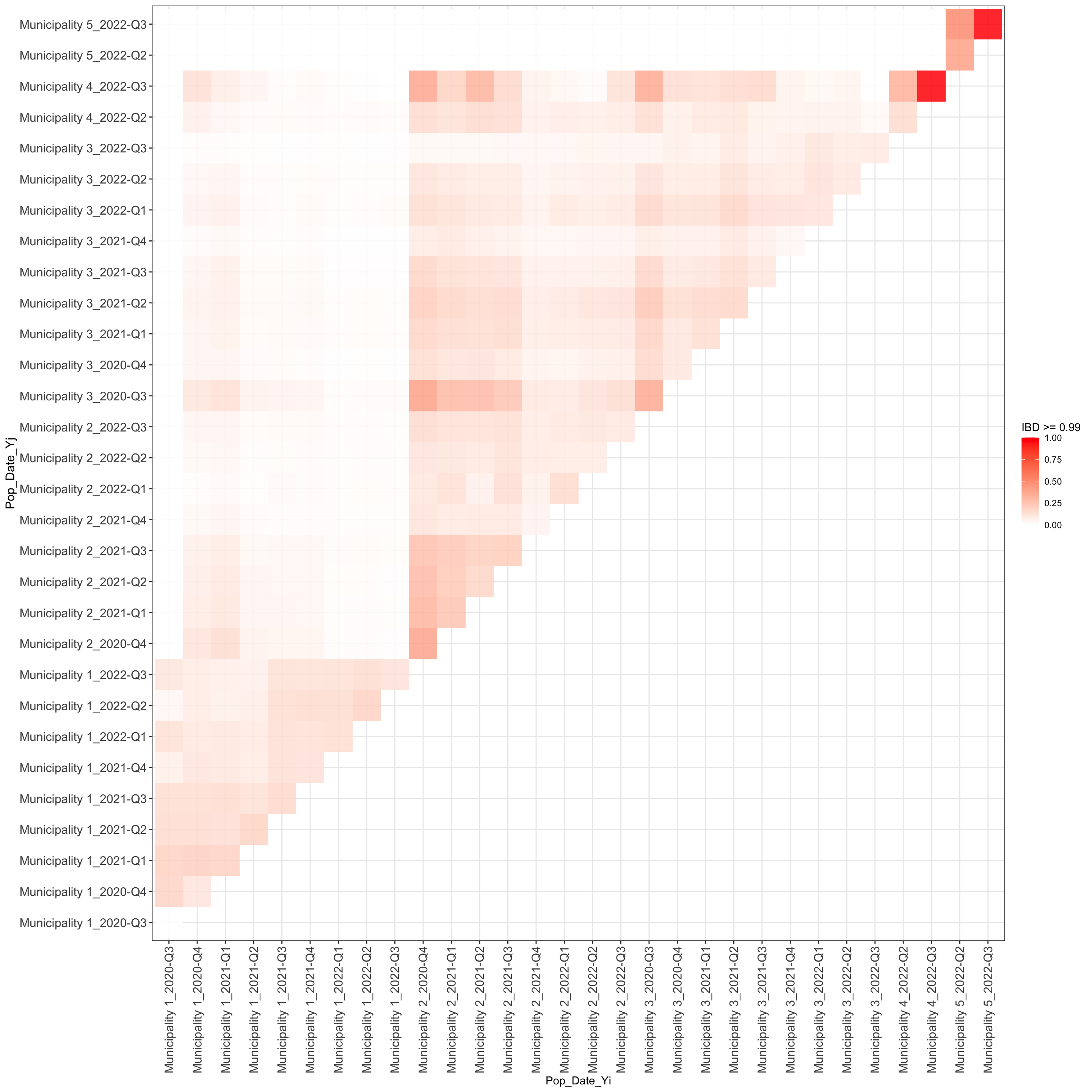
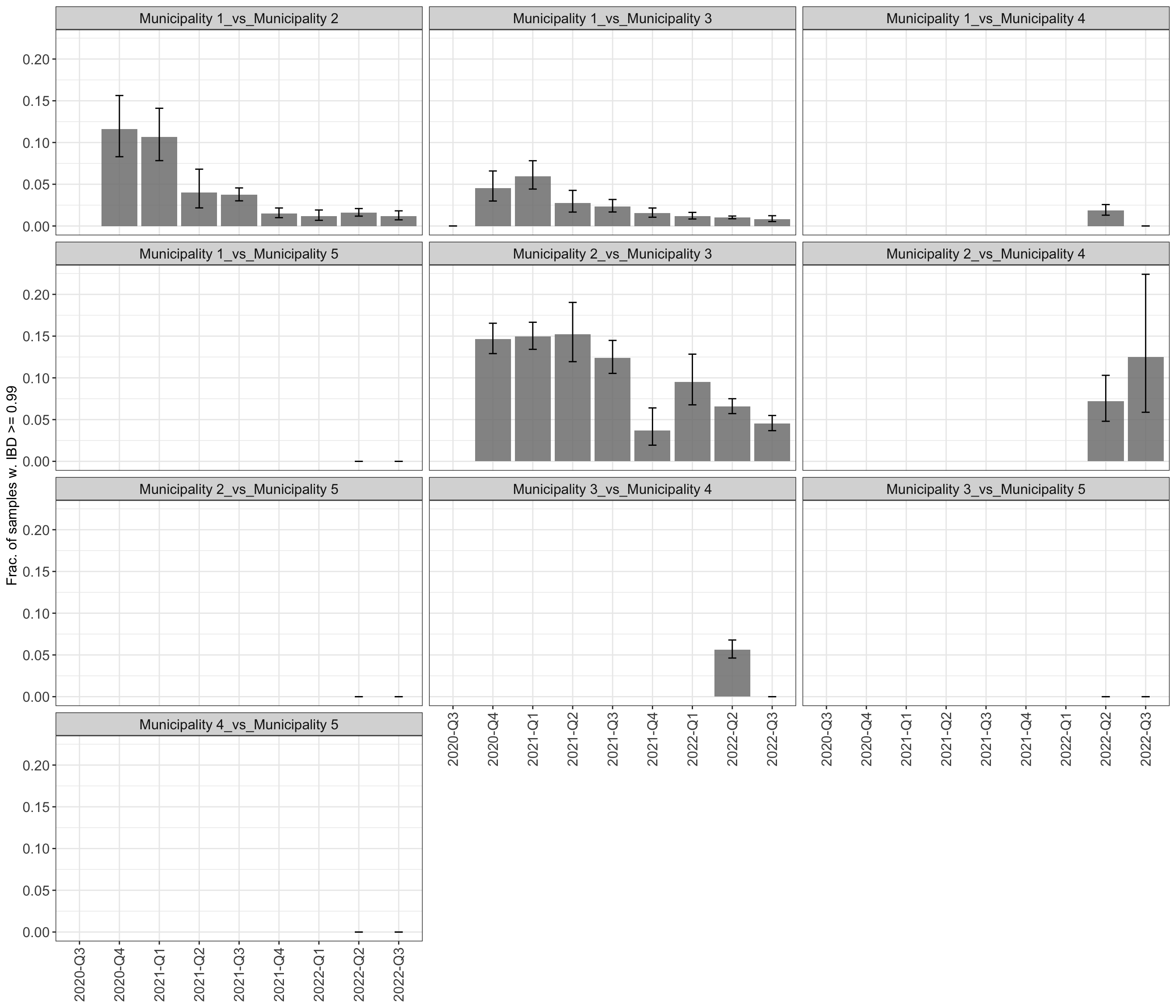
These values are presented in the following table and in Figures
3-4:
View(plot_frac_highly_related_overtime_between$frac_highly_related)
plot_frac_highly_related_overtime_between$plot_IBD_correlation_matrix
plot_frac_highly_related_overtime_between$plot_frac_highly_related
Finally, let’s create PCoA and network plots summarizing the genetic
relatedness between samples.
evectors_IBD = IBD_evectors(ampseq_object = ampseq_object,
relatedness_table = pairwise_relatedness,
k = length(unique(ampseq_object@metadata$Sample_id)),
Pop = 'Subnational_level2', q = 2)
col_vector = brewer.pal(5, 'Accent')
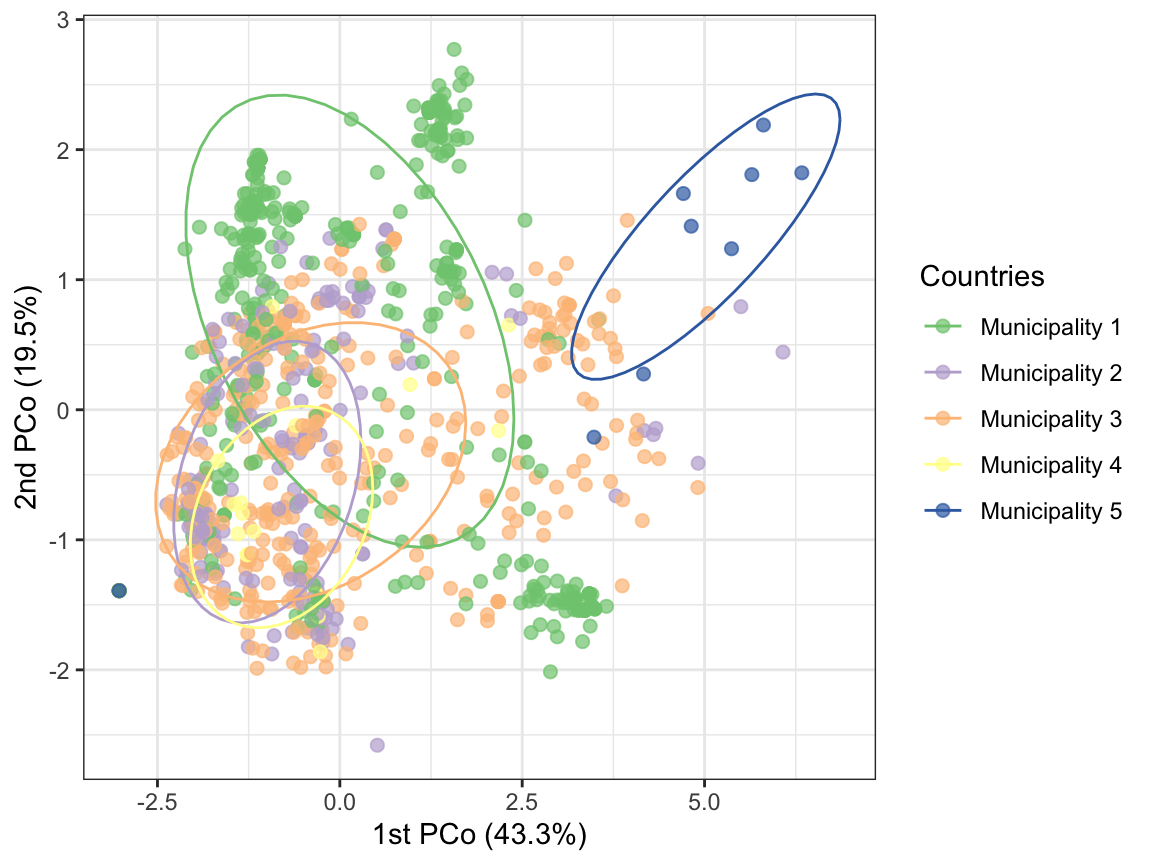
IBD_PCA = evectors_IBD$eigenvector %>% ggplot(aes(x = PC1, y = PC2, color = Subnational_level2))+
geom_point(alpha = .7, size = 2) +
stat_ellipse(level = .6)+
scale_color_manual(values = col_vector)+
theme_bw()+
labs(x = paste0('1st PCo (', round(evectors_IBD$contrib[1],1), '%)'),
y = paste0('2nd PCo (', round(evectors_IBD$contrib[2],1), '%)'),
color = 'Countries')
IBD_PCA
plot_network(pairwise_relatedness,
threshold = 0.99,
metadata = ampseq_object@metadata,
sample_id = 'Sample_id',
group_by = 'Subnational_level2',
levels = levels(as.factor(
ampseq_object@metadata[['Subnational_level2']])),
colors = col_vector
)
## $network_object
## IGRAPH eb1377a UN-- 1146 44031 --
## + attr: name (v/c)
## + edges from eb1377a (vertex names):
## [1] ID00001--ID00002 ID00001--ID00003 ID00001--ID00007 ID00001--ID00008
## [5] ID00001--ID00009 ID00001--ID00010 ID00001--ID00011 ID00001--ID00014
## [9] ID00001--ID00015 ID00001--ID00019 ID00001--ID00020 ID00001--ID00023
## [13] ID00001--ID00024 ID00001--ID00027 ID00001--ID00028 ID00001--ID00029
## [17] ID00001--ID00032 ID00001--ID00040 ID00001--ID00042 ID00001--ID00044
## [21] ID00001--ID00046 ID00001--ID00048 ID00001--ID00050 ID00001--ID00252
## [25] ID00001--ID00255 ID00001--ID00257 ID00001--ID00260 ID00001--ID00816
## [29] ID00001--ID00817 ID00001--ID00818 ID00001--ID00819 ID00001--ID00820
## + ... omitted several edges
##
## $plot_network
## NULL